OCT와 푸리에(Fourier)

조영재 / 현) 안산연세안과 원장, 전) 실로암 안과병원

OCT (Optical Coherence Tomography)는 1991년 미국 MIT의 J.G.Fujimoto에 의해 최초로 개발된, 근적외선을 사용하여 비침습적으로 생체조직의 단층영상을 얻을 수 있는 기기로 안과에서는 1993년 Fercher, Swanson 등에 의해 망막분야에 적용되었다.

OCT는 안과영역에서 비침습적으로 망막의 internal microstructure를 시각화(visualization)한다는 장점으로 인해 빠르게 진단의 optical imaging modality가 되었고, 이후 다양한 OCT기기의 개발과 더불어 수많은 연구 및 임상적용을 통해 현재 OCT는 망막질환의 진단에 중추적인 역할을 하고 있다.

특히 최근에 국내에 도입된 FD (Fourier Domain)-OCT는 기존의 TD (Time Domain)-OCT에 비해 100-1000배 정도의 향상된 감도와 수십 배의 고속촬영속도로 인해 기존에 구별이 쉽지 않았던 망막의 모든 layer에 대한 정보를 줄 수 있게 되었고, 이 때문에 망막을 거의 세포 수준에서 시각화하는 것이 가능하여 기존에 잘 알지 못했거나 잘못 이해되었던 여러 질병들에 대한 올바른 이해 및 병태생리학적 측면에서의 증명이 가능하게 되었다.

그렇다면 TD-OCT와 FD-OCT의 차이가 무엇이길래 이렇게 고해상도 영상을 제공할 수 있을까?

거기에는 Fourier가 있다. (Figure 1)

Fig.1 Jean-Baptiste Joseph Fourier

푸리에(Jean-Baptiste Joseph Fourier: 1768-1830)는 1768년에 태어난 프랑스의 수학자이자 물리학자이다. 그는 고체 내에서의 열전도에 관한 연구로 열전도 방정식(푸리에 방정식)을 유도하였으며, 이 방정식을 풀기 위해서 푸리에 해석이라 불리는 이론을 전개했다. 푸리에 해석은 복잡한 주기함수를 보다 간단한 함수의 합으로 표현할 수 있어 소리나 빛 등의 파동 연구에 넓게 이용되며 현재 조화 해석이라고 하는 수학의 한 분야를 형성하고 있다.

대개 신호(single wave)를 표현하고자 할 때 시간의 축에서 표현을 한다. 그러나 시간의 축이 아닌 주파수 축에서 보더라도 target이 되는 신호는 같은 신호일 것이므로, 주파수 축의 관점에서 재 해석 해보자는 것이 푸리에의 이론이고, 푸리에 변환은 시간과 주파수 신호를 서로간의 domain으로 변환이 가능하도록 해주는 변환이다. 이러한 변환이 가능하도록 해주는 이론은 하나의 신호는 정현파(sine wave)들의 합으로 표현이 가능하다는 푸리에 급수에 기인하고 있다.

사실 이러한 푸리에 변환은 우리 일상생활에서 복잡한 모양의 파동을 진동수나 진폭이 다른 단순한 파동들의 합으로 나타내 잡음 제거나 목소리 구별, 영상 노이즈 제거 등에 다양하게 활용되고 있다.

예를 들어 간섭현상을 이용하면 여객기 밖은 엔진에서 발생하는 소음으로 엄청나게 시끄럽지만, 여객기 안은 소음을 크게 느낄 수 없다. 또 경비행기 조종사나 수동 굴착기 기사는 소음을 줄이는 특수한 헤드폰을 끼는 덕분에 시끄러운 환경에서도 일을 할 수 있다. 이것은 능동소음제어(Active Noise Cantrol)라 불리는 기술이 적용되었기 때문으로 비행기 엔진이나 굴착기에서 나는 소음과 같은 주파수를 가지고 위상이 반대인 소음을 발생시켜 소음을 없앤다. 즉 소음을 소음으로 없애는 것이다. 최근 출시되는 고급 차량에도 이러한 소음제거기가 부착되어 정숙한 주행을 할 수 있게 해준다고 한다. 또한 주파수별로 파를 분리하면 사람의 목소리를 구분하는 음성인식에도 사용할 수 있다. 목소리는 지문과 같이 고유한 것이라‘성문’이라 부르는데 주파수 별로 나누어 비교하면 차이점이 뚜렷하게 나타난다.

또 푸리에 변환을 좀더 빠르게 수행할 수 있는 알고리즘인‘고속 푸리에 변환’이 없었다면 첨단 의료 장비인 CT는 만들어지지 못했을 것이다. CT는 X선을 방출하는 스캐너를 환자 주변으로 360도 회전시키면서 신체 내부에 대한 단면 사진을 얻는다. X선 스캔에 의해 얻어지는 정보는 단지 신체 내부에 대한 밀도분포 함수인데, 이 함수에서 영상을 조합해 내는데 바로 푸리에 변환이 사용된다. 또한 자기공명영상(MRI)도 마찬가지로 푸리에 변환이 사용된다. 기상학자들은 복잡한 기후의 변화를 연구할 때 푸리에가 없으면 아무것도 할 수 없을 정도이다. 이와 같이 우리 주변에는 푸리에 수학의 도움을 받는 분야가 너무 많다.

TD-OCT의 원리는 초발광다이오드(superluminescent diode)를 light source로 사용하여 beam splitter를 통해 안구조직에서 반사된 sample beam과 reference mirror를 통해 반사된 reference beam이 photo detector에 가게 되고 이곳에서 받은 2 wave가 서로 간섭현상을 일으키게 되고 이 진폭을 이용하여 영상을 얻게 되는 것이다. (Figure 2 & 3)

Fig.2 각각의 반사된 signal을 망막에서의 깊이와 reference mirror위치에 따라 다른 시간에 받는다.(T1,T2,T3….)
-출처 OCT in AMD by Gabriel COSCAS

Fig.3 Time-domain OCT의 기본원리
-출처 OCT in AMD by Gabriel COSCAS

이러한 시스템은 scanning과 각 section들의 획득에 필요한 시간이 signal quality를 결정하는 요소이므로 time-domain이라 불린다.

이에 반해 FD-OCT는 TD-OCT와 달리 reference mirror를 전후방향으로 scan할 필요 없이 고정시키고 검출기로 기준빔과 시료빔의 결합인 간섭신호의 분광 스펙트럼을 얻어 이를 시간영역으로 Fourier 변환하면 시료 깊이에 따른 OCT영상을 얻을 수 있는 것이다. (Figure 4 & 5)

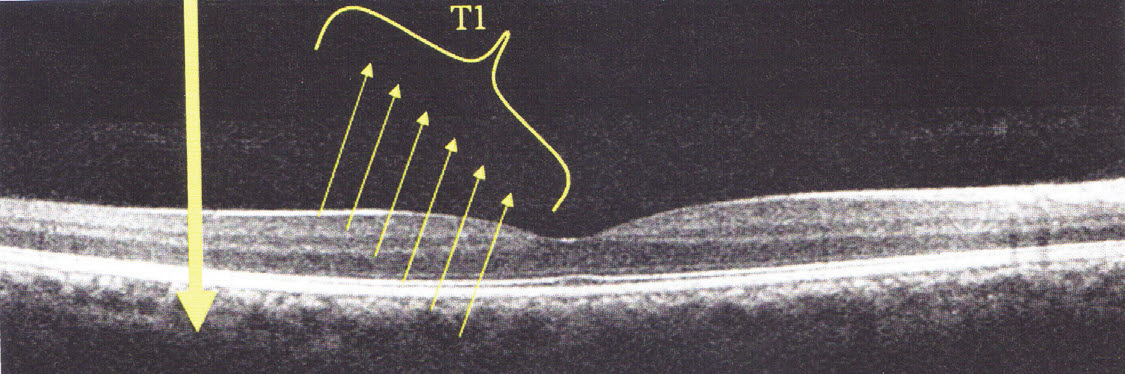
Fig.4 망막의 다양한 layer에서 반사된 모든 signal들을 동시에 spectrometer에서 받게 된다.
-출처 OCT in AMD by Gabriel COSCAS

Fig.5 Spectral-domain OCT의 기본원리
- 출처 OCT in AMD by Gabriel COSCAS

이러한 시스템에서의 간섭신호는 wavelength의 함수이므로 망막 모든 층의 신호가 동시에 측정될 수 있어 TDOCT보다 훨씬 빠르고, 훨씬 좋은 해상도 및 3차원 영상까지 얻을 수 있는 것이다.

FD-OCT는 사용하는 광원에 따라 광대역광원을 사용한 SD-OCT (Spectral Domain OCT)와 파장가변레이저로부터의 레이저광을 사용하는 SS-OCT (Swept Source OCT)로 분류될 수 있으나 우리들이 사용하는 대부분의 OCT는 광대역광원을 사용하므로 FD-OCT를 SD-OCT와 혼용해서 사용하고 있다.

또한 FD-OCT는 신호강도뿐만 아니라 위상정보를 얻을 수 있는 이점이 있어 이를 이용하여 도플러 FD-OCT, 편광에 민감한 편광 FD-OCT의 영상을 얻을 수도 있다.

또한 이러한 OCT는 앞으로 구조적인 정보뿐 아니라 외부자극에 의한 변화를 측정하는 기능적인 정보를 결합한 functional OCT로의 발전으로 보다 많은 정보를 줄 것이라고 생각된다.

- 출처 : 안과학회소식_대한안과학회_201012_통권141호_제14권_12호